ところで「グラフ」ってどういう意味？ #Neo4j #GraphDatabase #グラフデータベース #ビギナーのためのグラフデータベース

本ブログは、Neo4j社のブログで Neo4j ブログの編集者であるEnzo Htet氏が執筆し、2019年12月16日に公開された「Graph Databases for Beginners: Wait, What Do You Mean by “Graph”?」の日本語翻訳です。

この「ビギナーのためのグラフデータベース」ブログシリーズでは、グラフテクノロジーに関するバックグラウンドがほとんどない（または全くない）方を想定して、グラフテクノロジーの基本を解説していきます。
 
今回は、「グラフとは何か」と「そうでないもの」を定義することから始め、誰でもこのモデルを理解できるように説明します。

はじめに

私は、大学の数学の授業で、初めて巡回セールスマン問題に出会いました。

これは 「目的地のリストと各都市間の距離が与えられたとき、セールスマンが各都市を訪問してスタート地点に戻るための最短経路は何か？」 といった古典的な問題です。
図1にその例を示しています。

 
私は数学が苦手で、単なる2次方程式を見ると、「穴を掘って、入って、出たくない」と思ってしまうのです。
しかし、この問題は違っていました。巡回セールスマンで「すべての都市を回って同じ場所にたどり着く最短ルートを見つけろ」と言われたとき、私はクラスメイトの数学オタク全員を打ち負かすことができました。

その時、初めて「グラフ」を見たのですが、数学って面白いな〜と思いました。

グラフとチャート

「グラフ」という言葉は、あなたが思っているような意味ではありません。

もしあなたが大学で数学やコンピュータサイエンスを学んでいないのなら、「グラフ」の定義がを勘違いしていても無理はありません。一般常識では、この言葉はまったく違う意味で使われているため、言葉の定義を少し分類してみましょう。

グラフと言われてまず思い浮かべるのは、代数学の授業で、xとyの座標を使って変数を線上にプロットした図かもしれません。こんな感じです：

 
でも...これって、実は「グラフ」じゃないんです。私たちが取り組んでいるコンピュータサイエンスやテクノロジーの分野では「グラフ」ではありません。

また、多くの人は次のようなものを思い浮かべるかもしれません：

 
しかし、図3も「グラフ」ではありません。一般に折れ線グラフと呼ばれていますが、今日お話しする「グラフ」とは違います。
折れ線グラフは、実は以下のような表の一種に過ぎないのです：

 

上の画像はどれも「グラフ」ではなく、「データチャート」という種の図表です。チャートとは、データを視覚化したもので、多くの場合、統計的なもので、折れ線グラフ、棒グラフ、円グラフ、レーダーチャート、ヒートマップなどがあります。

では、「グラフ」とはどのようなものなのでしょうか。実際の「グラフ」は次のようなものです：

 

グラフとは何か？

グラフとは、ものごとのネットワークであり、ものごとが互いにどのように関連しているかを示すものです。グラフは、ノードとリレーションシップという2つの基本単位で構成されています。

ノード（Node）とは何か？

ノードは、エンティティ、つまり、人・場所・物・システム・ことがら、その他あらゆる"もの・ごと"を表します。
最もシンプルなグラフは、1つのノードです。例えば、こんな感じです:

 

このグラフは1つの「リオネル・メッシ」を表すノードで構成されています。このグラフは、このままでは、リレーションシップも他のノードも持っていません。
しかし、このグラフは、より複雑で豊かな相互のつながり構造を持つように他のグラフと接続することができます。

リレーションシップ（Relationship）とは何か？

グラフでは、リレーションシップ（または、エッジと呼ぶ）が2つのノードを接続します。

リレーションシップは、ノードをつなげて構造を生み出すことで、リレーションシップでつなげられたノードすべてに"コンテキスト"(新たな意味や付加価値)を与えます。リレーションシップによって、グラフはリスト・ツリー・マップ・複合体・二重螺旋DNA・マネーロンダリングの繋がり・企業組織構造などなどを模倣(モデリング)することができます。

先の「リオネル・メッシ」の単独ノードグラフは、ノードとリレーションシップを追加することで、以下のようにより新たな意味を持つようになります：

 

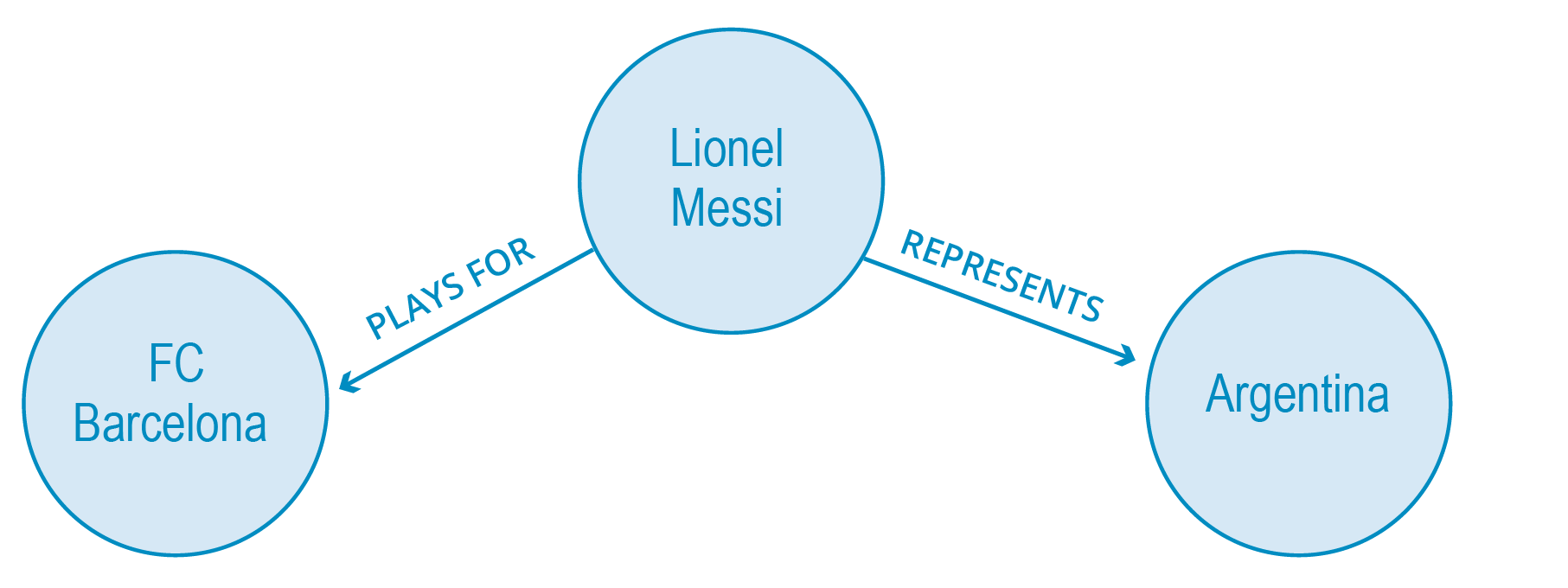
このように、わずか数個のノードとそれらをつなぐリレーションシップによって、高度な"コンテキスト"があるモデルを簡単に理解できるようになります。

グラフ理論の基礎知識

グラフ理論とは何でしょうか？それはグラフ（ノードとリレーションシップからなるネットワーク）の数学的特性をまとめた知識系統です。

ノードとリレーションシップに関したこの数学分野は、スイスの数学者であるレオンハルト・オイラーが1735年にケーニヒスベルクの橋の問題を解いたときに発見されました。
（この古典的なグラフ問題は、すでにご存知だと思うので手短に説明します。）ケーニヒスベルク市(図11)では、7つの橋すべてをそれぞれ1度だけ渡って市内を巡るルートを見つけるという挑戦がありました。オイラーは数学の力で、そのような道は存在しないことを証明し、その結果、グラフ理論の最初の定理を発見しました。

図11：ケーニスベルクの7つの橋 - 各橋を1回ずつ（しかも1回だけ）渡る道を見つけるのは、よくある課題だった。オイラーはグラフ理論を使って、そのような道を見つけることが不可能であることを証明した。
Bogdan Giuşcă, CC BY-SA 3.0, ウィキメディア・コモンズ経由で

 

今日、グラフ理論は、想像以上に多くの分野で使われています。

コンピュータサイエンスでは、アルゴリズムやプログラムをモデル化し、開発するためにグラフを使用します。化学者は、化学構造をモデル化するためにグラフを使用します。社会科学の分野では、ソーシャルネットワーク分析によって、人々の相互作用や関係性を研究するためにグラフが使われています。グラフ理論は娯楽にも利用されています。パズルゲームの多くはグラフ問題であり、多くのゲーム製作者がオイラーグラフやハミルトングラフのパズルを応用して商品を生み出しています。

そして、グラフの最も強力なアプリケーションの1つは、データベース管理システムです。

グラフをデータベースに活用する

多くの人が「データベース」という言葉を使うとき、私たちが最初に思い浮かべるのは、下の画像のようなテーブル（表）の集合です。

 

テーブルを思い浮かべるのは、1970年代以降、データベースの世界はリレーショナル・データモデルを中心に回ってきたからです。しかし、データベースはテーブルとイコールである必要はありません。(※ 「リレーショナル」は代数学の用語であり、リレーションシップとは無関係です。数学者の中には、名前をつけるのが苦手な人もいたのです。)

さて、従来のリレーショナル・データベースモデルのことは忘れてください。

スウェーデンの数学オタクのおかげで、データベースは標準的なリレーショナルモデルだけでなく、グラフモデルを利用することができるようになりました。グラフを使えば、バックエンドエンジニアやアーキテクトは、接続指向のクエリに対して、より柔軟で効率的な方法でデータをモデル化することができます。こうして、グラフデータベースが誕生しました。

人、物、場所、カテゴリ、その他あらゆるデータを表すノードを描き、それらのデータ点を線で結んで、あるエンティティが他のエンティティとどのように関連しているかを示します。これで、データモデルが完成です。

 

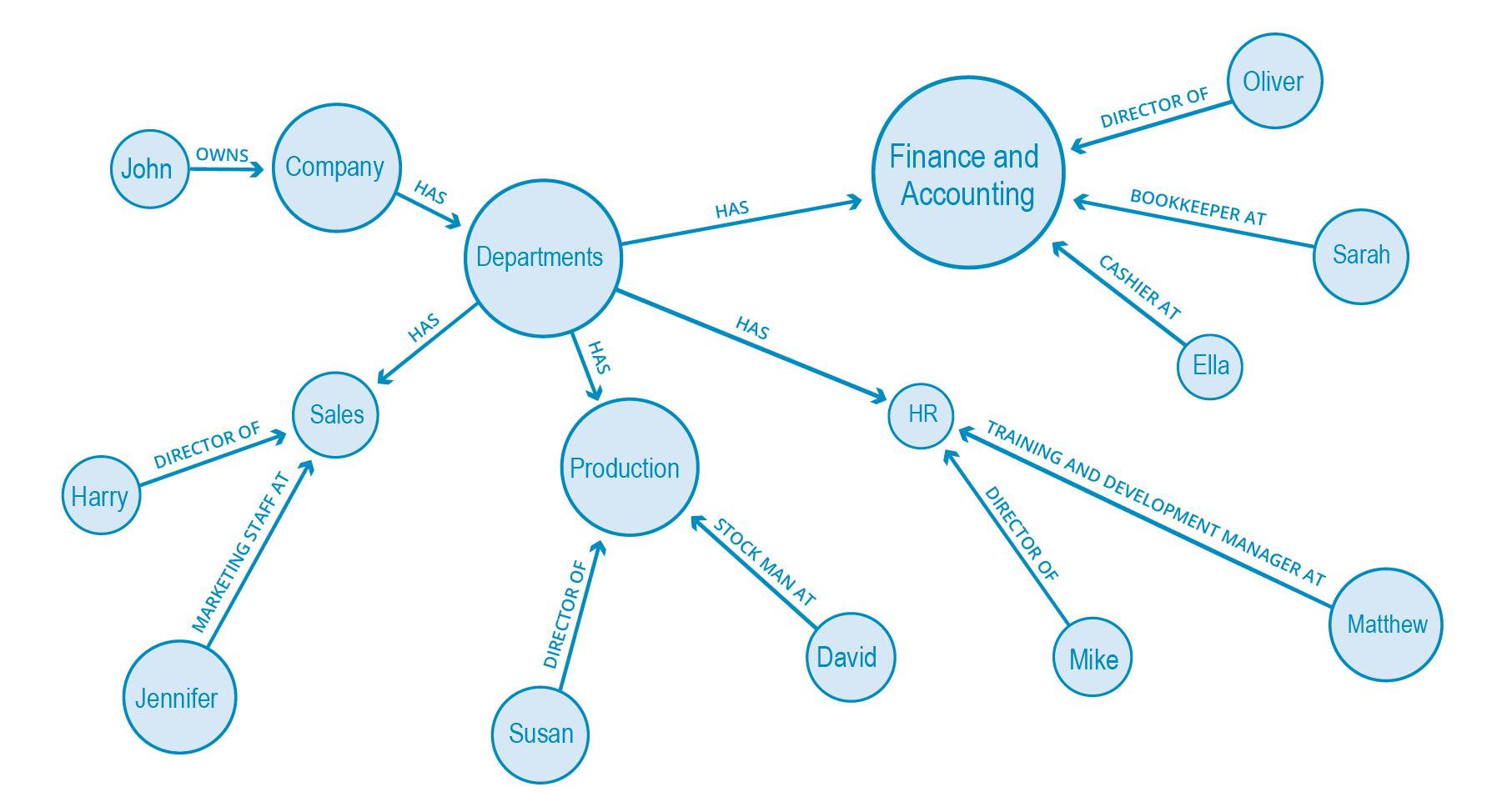
最終的には、子供でも理解できるほどシンプルな図ができあがります。

Google、Facebook、LinkedIn、PayPalといった巨大企業はビジネス帝国を築きました。その秘訣はグラフデータベース技術を使って、つながれたデータのパワーを活用したことです。

以上ですが、これはグラフデータベースの簡単な概要に過ぎません。グラフデータベーステクノロジーを定義し、その新しい世界に飛び込むには、別の記事（あるいはシリーズ）が必要です。

まとめ

過去3世紀にわたり、グラフ理論は他のさまざまな対象を研究したりモデル化するためのツールとして採用されています。数学の中でも、数字や方程式を解くのが得意でなくても活用できる、独特な分野の1つです。

しかし、グラフ理論がデータベースモデルとして取り上げられたのは、21世紀に入ってから（文字通り、2000年に入ってから）です。革新性、接続性、シンプルさが求められる日進月歩の世界では、敏捷性、柔軟性、性能を備えたグラフテクノロジーこそが「未来の技術」と言えるでしょう。

結局のところ、私たちが「グラフ」という言葉を使うとき、何を意味しているのでしょうか。それは「すべてがつながっている」ということです。

 

「ビギナーのためのグラフデータベース」ブログシリーズの一覧