Neo4j SandBox Graph Data Science プロジェクトを体験してみた（後編） #Neo4j #SandBox #GDS

本記事は先日投稿した前編からの続きです。

---

シナリオ4: Louvain Modularity 法 - コミュニティ（クラスタ）の検出

Louvain Modularity 法とは

中心性測定の他にも、グラフの中からコミュニティを検出する方法はたくさんあります。
コミュニティ検出はグラフの中からクラスタを検出するのに便利なツールです。
例えば、空港のルートのグラフにおいては、コミュニティの検出は相互につながる多数のルートによって自然に作られる空港のクラスタを検出するのに役立ちます。

このセクションでは、よく知られた Louvain Modularity 法によるコミュニティ検出について説明します。
このアルゴリズムは、リレーションの相対的な密度を計測することによって、グラフの中のクラスタを見つけます。
これは modularity スコアによって定量化されます。これは、クラスタ内の関係の密度を平均あるいはランダムサンプルから比較したものです。modularity が高くなれば、クラスタの密度は高くなります。
Louvain 法は反復的なアプローチによってグラフ全体にわたる modularity が最大になるように試みます。
PageRank と同様に、GDS において、ユーザは反復回数の最大値と、反復の早期終了のための許容値を指定することが可能です。加えて、アルゴリズムは、収束の途中で中間コミュニティ割り当てを返すことができます。

Louvain Modularity 法のサンプル

stream モードを使用してアルゴリズムの結果を調べてみましょう。下記のクエリを使用します。

CALL gds.louvain.stream('routes')
YIELD nodeId, communityId
RETURN
    communityId,
    SIZE(COLLECT(gds.util.asNode(nodeId).iata)) AS number_of_airports,
    COLLECT(gds.util.asNode(nodeId).city) AS city
ORDER BY number_of_airports DESC, communityId;

このケースでは、community ID を取得し、結果のリストを生成する 'COLLECT' とリストのサイズを返す 'SIZE' の組み合わせによって、それぞれのコミュニティに属する空港の数とそれぞれのコミュニティに属する都市のリストを取得します。
結果は下記のようになります。

リストを調べると、最も大きな空港のコミュニティはアメリカにあり、次に大きな空港のコミュニティはヨーロッパにあることがわかります。空港が大陸によってクラスタ化されているように見えるのは理にかなっていると言えるでしょう。
これらの結果をノードプロパティとして書き込みたい場合は、'gds.louvain.write()' を使用します。

---

シナリオ5: Jaccard係数 - ノード類似度の測定

ノード類似度について

中心性の測定やコミュニティの検出と同様に、ノード類似度を計算するには様々な方法があります。
一般に、ノード類似度は様々なベクトルベースのメトリクスを使用してノードのペアに対して計算されます。
ノード類似度は、例えば、顧客の購入履歴に基づいて似たような商品をレコメンドするレコメンドエンジンなどのために役立ちます。

このセクションでは、Jaccard 類似性スコアの一般的アプローチを使用する GDS ノード類似度のアルゴリズムを試します。
このシナリオで扱っている空港間グラフは、ノード類似度を計算する対象として理想的なグラフではないかもしれませんが、このセクションで行うアプローチは一般的なものです。

Jaccard ベースのノード類似度は、ノードのペアにより共有される隣接ノードの数を参照します。今回の場合では、隣接ノードとは外向きのリレーションでつながっている全てのノードのことを指します。ペアをなしている2つのノードで共有される隣接ノードの数が大きくなればなるほど、類似度は高くなります。そして、類似度の最小値は0(共有される隣接ノードがない)であり、類似度の最大値は1(全ての隣接ノードが共有されている)です。

ノード類似度の計算時間はグラフに含まれるノードの数に対して2次関数的に変化することに注意してください。
大きなグラフでの実行時間を短くするために、ノードの次数（外向き/内向きのリレーションの数）および類似度に限界値を設けることもできます。これにより、評価対象のペアの組み合わせの数が減ります。
次に述べるように、制限値はグラフ全体に対して設定することもできますが、ノードごとに設定することもできます。

ノード類似度のサンプル

非常に基本的なノード類似度の計算例を見てみましょう。

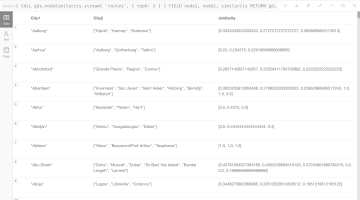
CALL gds.nodeSimilarity.stream('routes')
YIELD node1, node2, similarity
RETURN
    gds.util.asNode(node1).city AS City1,
    COLLECT(gds.util.asNode(node2).city) AS City2,
    COLLECT(similarity) AS similarity
ORDER BY City1

結果は下記のようになります。

このアルゴリズムはグラフに存在するそれぞれの空港ノードについて最も類似度の高い10のノードを返します。デフォルト値10を取る topK という構成パラメータによって、ノードあたりの結果の個数（K）が制限されています。

クエリを下記のように変更することで、ノードあたりの結果の個数を3個以下に制限することができます。

CALL gds.nodeSimilarity.stream(
    'routes',
    {
        topK: 3
    }
)
YIELD node1, node2, similarity
RETURN
    gds.util.asNode(node1).city AS City1,
    COLLECT(gds.util.asNode(node2).city) AS City2,
    COLLECT(similarity) AS similarity
ORDER BY City1

結果は下記のようになります。

また、構成パラメータ topN を指定することで、グラフ全体での結果の個数（N）を制限することもできます。
下記の例では、グラフ全体で最も類似度の高い20個のノードを返します。（ノードあたりの結果の個数の制限は topK のデフォルト値10が採用されています）

CALL gds.nodeSimilarity.stream(
    'routes',
    {
        topN: 20
    }
)
YIELD node1, node2, similarity
RETURN
    gds.util.asNode(node1).city AS City1,
    COLLECT(gds.util.asNode(node2).city) AS City2,
    COLLECT(similarity) AS similarity
ORDER BY City1

結果は下記のようになります。

※topKとtopNは同時に設定することもできます。

次数と類似度に限界値を設定する

計算量を制限する別の方法は、計算の全体にわたって考慮されるノードの次数の最小値を与えることです。
例えば下記の例では、空港に出入りするフライトが最低100回以上あることを要求します。

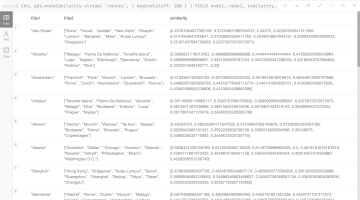
CALL gds.nodeSimilarity.stream(
    'routes',
    {
        degreeCutoff: 100
    }
)
YIELD node1, node2, similarity
RETURN
    gds.util.asNode(node1).city AS City1,
    COLLECT(gds.util.asNode(node2).city) AS City2,
    COLLECT(similarity) AS similarity
ORDER BY City1

結果は下記のようになります。

また、類似度スコアの最小値を設定することもできます。

CALL gds.nodeSimilarity.stream(
    'routes',
    {
        similarityCutoff: 0.5
    }
)
YIELD node1, node2, similarity
RETURN
    gds.util.asNode(node1).city AS City1,
    COLLECT(gds.util.asNode(node2).city) AS City2,
    COLLECT(similarity) AS similarity
ORDER BY City1

結果は下記のようになります。

---

シナリオ6: ダイクストラ法 - 経路探索

経路探索とは

経路探索の主な目的は、2つ以上のノードの最短経路を見つけることです。このシナリオで扱っている空港間グラフの場合は、空港のつながりに対して、フライトの全行程を最小化する経路を特定します。

このセクションでは、よく知られたダイクストラ法によって2つのノード間の最短経路を見つけます。ここで初めて、重み付きのプロジェクショングラフが必要になります。

ダイクストラ法は、ソースノードからそれに直接つながる全てのノードに対し、最小の重みを持つリレーションを見つけることから始まります。そして、ソースノードにつながっているノードに直接つながる全てのノードに対し、同じ計算を行います。このプロセスを繰り返し、ターゲットノードにたどり着くまで、常に最小の重みを持つリレーションを選び続けます。

重み付きプロジェクショングラフを生成する

前の例では、2つの空港の距離を考慮に入れませんでした。今回は距離に基づいて最短経路を計算します。
まず、2つのノード間のリレーションの重みとして距離を使用し、プロジェクショングラフを作成します。
リレーションの重みを付け加えること以外は、前の例と全く同じです。

CALL gds.graph.project(
    'routes-weighted',
    'Airport',
    'HAS_ROUTE',
        {
            relationshipProperties: 'distance'
        }
)

ダイクストラ法のサンプル

重み付きプロジェクショングラフを使用して、デンバー国際空港（DEN）からマレ国際空港（MLE）までの最短距離を計算してみましょう。

MATCH (source:Airport {iata: 'DEN'}), (target:Airport {iata: 'MLE'})
CALL gds.shortestPath.dijkstra.stream('routes-weighted', {
    sourceNode: source,
    targetNode: target,
    relationshipWeightProperty: 'distance'
})
YIELD index, sourceNode, targetNode, totalCost, nodeIds, costs, path
RETURN
    index,
    gds.util.asNode(sourceNode).iata AS sourceNodeName,
    gds.util.asNode(targetNode).iata AS targetNodeName,
    totalCost,
    [nodeId IN nodeIds | gds.util.asNode(nodeId).iata] AS nodeNames,
    costs,
    nodes(path) as path
ORDER BY index

結果は下記のようになります。

上記のクエリを見ると、ソースノードとターゲットノードを指定し、distance を relationshipWeightProperty として使用していることがわかります。
このクエリから、多くの結果が返ってきます。それは、全コスト（distance の合計で、通常はタキシング時間等の潜在的な時間の遅れを無視した直線距離を表します）や、経路に含まれる空港のリストを含みます。
このケースでは、最短経路は4ホップの長さです。実用的ではないかもしれませんが、これは distance の合計値が最小となる経路です。

---

終わりに

与えられたグラフに対して適切なアルゴリズムを使用する

全ての GDS アルゴリズムが全てのプロジェクショングラフのタイプで実行できるわけではありません。
一部のアルゴリズムは、Heterogeneous Graph（ノードにいくつかの種類がある、あるいはエッジがいくつかの異なる関係を表すグラフ）よりも Homogeneous Graph（全てのノードが同じ性質を持ち、全てのエッジが同じ意味合いの関係を表すグラフ）を優先します。無向グラフでのみ正しく機能するアルゴリズムもあります。重み付きリレーションでは動作しないアルゴリズムもあります。
API ドキュメントを参照して選んだアルゴリズムがグラフに適切なものかどうか確認してください。

クリーンアップ

メモリを解放するために使わなくなったプロジェクショングラフを削除するのを忘れないでください！

CALL gds.graph.drop('routes');
CALL gds.graph.drop('routes-weighted');

以上のシナリオで、どのようにグラフアルゴリズムが動作するかについての基本を確認し、ごくわずかな種類の基本的なアルゴリズムでそのアプローチを示しました。
他のアルゴリズムや設定項目についての詳細は、GDS ドキュメントを参照してください。