天気データのみで電力を予測する：線形回帰編

こんにちは、クリエーションラインの朱です。最近はどんな業界でも、どんな会社でもAIという言葉を使い始めましたね。こんな熱いAIの分野で、新人でもありますが、日々精進しています。
今回は「重回帰で時系列データを扱う」というテーマで機械学習の話をしたいと思います。

まず僕のような新人のために重回帰が何かを直感的に簡単に説明します。

／1a+2b=3
＼2a+5b=8
上記のaとbを求めてくださいのような中学ラベルの数学問題が見たことがあると思います。

今回のテーマは天気データのみで電力を予測するということなので、書き換えると以下のテーブルになりますね。

気温	降水量	電力
1	2	3
2	5	8

方程式が以下になります。

a☓気温＋b☓降水量＝電力

統計的手法で上記説明変数「気温」の係数aと説明変数「降水量」の係数bを求めるのが回帰です。ここが多変数なので、重回帰になります。電量は目的変数と呼びます。
統計的手法とは具体的にコスト関数を設定して、コスト関数の値が最小になるようにa,bを調整して行く手法ですが、詳細を説明すると長くなるので割愛します。
上記の方程式をモデルと呼びます。最適なモデルを作ることで、天気予報を方程式に代入することで未来の電力を予測できるわけです。

話を戻します。人間が時間軸で生きていますから、電力データのような時系列データが多いですが、実際に時系列データの分析では、多変数の分析が難しく、単一変数の分析が多いようです。
重回帰を使うと、多変数の時系列データ分析が可能ですが、回帰を正しく行うためには、扱うデータが独立仮説（Assumption of Independence）に従わなければならないです。
時系列データは基本独立仮説に従わないので、従うようにfeature engineeringが必要ですし、データのトレンドを考量した学習アルゴリズムを選択することによって独立仮説の問題を解消することが可能です。

独立仮説とは、データが以下の条件に満たしていると仮定します。
1. 説明同士が独立であります。天気データで例えると、気温と日照量が強く関係しているので、両方を同時に説明変数として使うと、独立仮説に違反します。
2. 一つの説明変数のデータ同士の間が独立であります。例えば明日の来客数が今日の来客数に影響されない等。

但し、データが独立仮説に違反しないかを確認するには、データに関するドメイン知識が必要になりますし、データを可視化し、時系列データの季節調整を行うとか、機械学習の前処理が必要になります。
独立仮説の検証は今回の目的ではありませんので、確認せず、時系列データに対して重回帰を行いました。
では本題に入りたいと思います。

天気データのみで電力を予測する

自分自身は電力系のシステム開発を行った経験がありまして、電力の予測に興味があって、今回のテーマにしました。

早速データを取得します。

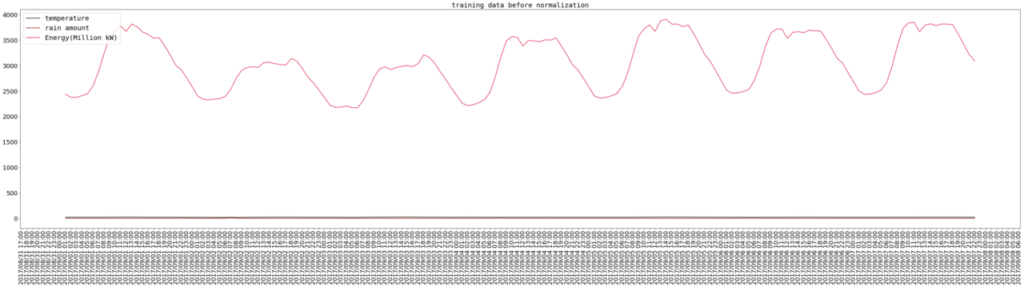
電力データと天気データを取得し、教師データ(80%)とテストデータ(20%)にわけます。

import pandas as pd

# tepcoから電力データを取得

energy_data_url="http://www.tepco.co.jp/forecast/html/images/juyo-2017.csv"

energy_data_df = pd.read_csv(energy_data_url, skiprows=[0, 1], encoding="shift-jis")

energy_data_df.columns = ["DATE", "TIME", "energy"]

energy_data_df["time"] = energy_data_df["DATE"] + " " + energy_data_df["TIME"] + ":00"
# 天気データを読みこむ

weather_data_df = pd.read_csv("./sample_data/weather_201709.csv",

                              skiprows=[0, 1, 2, 4],# dont skip 3rd row as it's the header

                              encoding="SHIFT-JIS")
# extract time, rain_amount, temperature data

weather_data_df = weather_data_df.iloc