ディープラーニングでBitcoinの価格を予測して見る #Deep Learning #Keras

こんにちは、クリエーションラインの朱です。

最近、ICO（Initial Coin offering）が非常にホットなキーワードになっています。文字通り、ICOは企業がプロジェクトの初期段階でコイン（仮想通貨）を使って資金を調達する仕組みです。ICOによってスタートアップでも簡単に事業を立てるための資金を調達できるようになりました。今回は仮想通貨の中でも特に有名なBitcoinの価格をディープラーニングで予測してみました。系列データの処理に得意とするRNN（Recurrent Neural Network）の一種であるLSTMを使用しました。

今回扱うデータがBitcoinの価格のみ、他のデータは一切使いませんでした。但し、結論から言うと、このままだと上手く予測できず、他のデータ（特徴量）が必要になります。今回は勉強が目的なので、特徴量を探すのはまた別の機会にしたいと思います。

今回の実装はKerasライブラリを使ってみましたが、所感としてはとにかくコーティングの量が少ないです。ディープラーニングの理論は複雑ですが、こんな短い期間で実装できるのが驚きです。

では、早速本題に入りたいと思います。

データを準備

データの取得

今回のデータは大手仮想通貨取引所のPoloniexから取ってきます。Python用のAPIが提供されているので、API経由で取得します。

import poloniex
import time
import pandas as pd
import matplotlib.pyplot as plt

def return_chart_data(pair, period, day):
    polo = poloniex.Poloniex()
    chart_data = polo.returnChartData(pair,
                                      period=period,
                                      start=time.mktime(time.strptime(start_time, "%Y-%m-%d %H:%M")),
                                      end=time.mktime(time.strptime(end_time, "%Y-%m-%d %H:%M")))
    df = pd.DataFrame(chart_data)
    df["datetime"] = pd.to_datetime(df["date"].astype(int) , unit="s")
    df = df.set_index("datetime")
    fig, ax1 = plt.subplots(figsize=(20, 10))
    ax1.plot(pd.to_datetime(df["date"].astype(int) , unit="s"),
             df["close"].astype(np.float32), label = "Coin Price", color="deeppink")
    ax1.legend(loc=2, fontsize=14)
    ax1.tick_params(labelsize=14)
    plt.show()
    return df

# USDT_BTCコインペアのデータを取得、データ間隔は300s、期間は2018-03-30 00:00から2018-04-01 00:00まで
data_df = return_chart_data("USDT_BTC", 300, "2018-03-30 00:00", "2018-04-01 00:00")

※余談ですが、ここのUSDTはUSDではなくTetherという仮想通貨です。しかもTetherが今流行な分散型ではなく集中型です。1Tether=1USDなので、USDとみなしても大丈夫です。

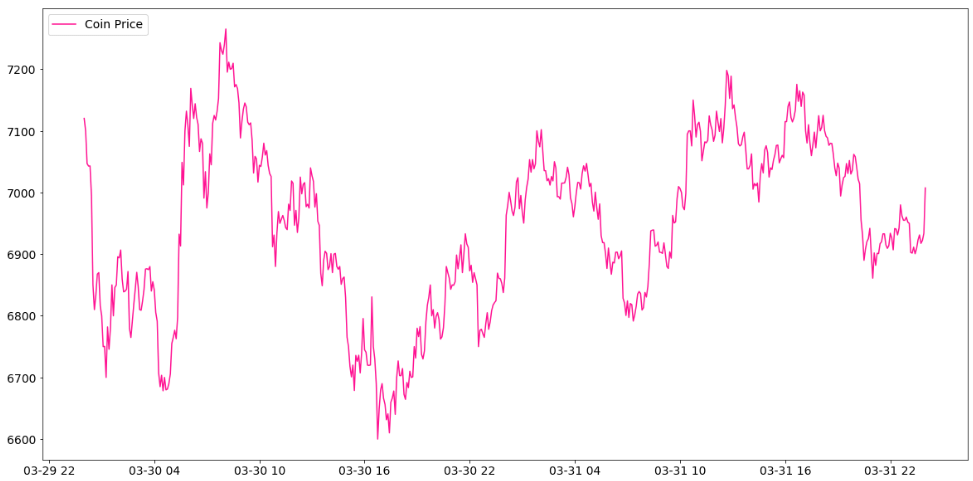
Poloniexから取得したデータのdateとclose列が今回の時系列データになります。以下はdateを横軸に、closeを縦軸にプロットしたグラフです。

データの階差を取る（differencing）

Bitcoin価格のようなファイナンシャルデータは基本Random walkの性質を持っています。Random walkとは以下のことを指します。
- 長期の下落か上昇のトレンドがある
- 急に予測不能な方向に変化することがある

こういう性質を持つデータを非定常データと呼びます。分析を行うためには、データからトレンドを抽出し、定常的なデータに変化させる必要があります。
ここでは、データのトレンドを取り除きます。階差（differencing）という手法を使いますが、以下の数式で行いますが、close_diffed(t)が時刻close(t)と時刻close(t-1)の階差になります。また、Bitcoin価格には特に周期性が見当たらないので、今回は隣接の時刻の階差を取りますので、階数が1になります。

close_diffed(t)=close(t)−close(t−1).

但し、後程の予測結果でお見せしますが、こういうやり方では、close(t)の予測結果がclose(t-1)の観測値と似たようなトレンドになります。予測が観測より一歩遅れている感じになります。
もしデータに周期性(季節性等)が存在するのであれば、かなり有力な方法です。

ソースコードは以下の通りです。

def difference_data(data_df):
    diff_interval = 1
    data = data_df["close"].values
    diff = np.empty((0,1), np.float32)
    for i in range(diff_interval, len(data)):
        value = data[i] - data[i - diff_interval]
        diff = np.append(diff, value)

    data_df = data_df.iloc[self.diff_interval:, :]
    return diff, data_df

data_diff, data_df = difference_data(data_df)

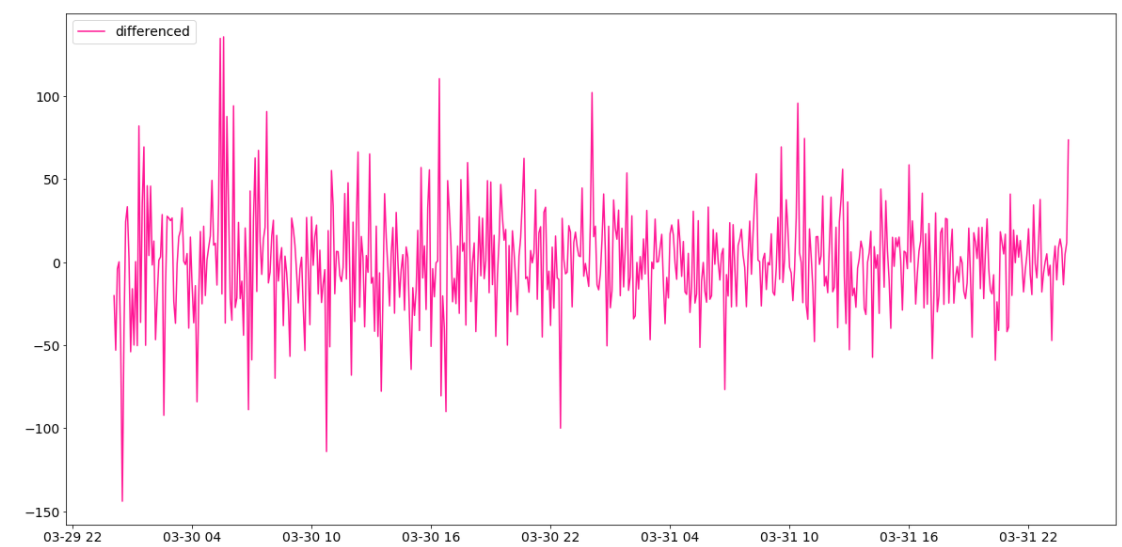
階差をとったデータが以下のグラフになります。

特徴量の準備

今回扱うデータがBitcoin価格のみなので、学習と予測を行うために、特徴量を作成する必要があります。
今回はt時刻のデータclose(t)の特徴量をclose(t-30)...close(t-1)の系列とします。これで一つの観測値にたいして30個の特徴量が得ました。
この後、close(t-30)...close(t-1)の系列でclose(t)を予測するわけです。

def generate_series_data_for_supervised_learning(data_array, datetime_array):
    t = np.empty((0,1), int)
    x = np.empty((0,30), np.float32)
    y = np.empty((0,1), np.float32)

    m = len(data_array)
    for n in range(30, m):
        new_t = np.array([[datetime_array[n]]])
        new_x = np.array([data_array[n-30: n]])
        new_y = np.array([[data_array[n]]])
        t = np.append(t, new_t, axis=0)
        x = np.append(x, new_x, axis=0)
        y = np.append(y, new_y, axis=0)

    self.dataframe = self.dataframe.iloc[30:, :]
    return t, np.concatenate([x, y], axis=1)

time_array, data_array = generate_series_data_for_supervised_learning(data_diff, data_df.index)

データの分割

今回は教師データ（交差検証データを含む）80%、テストデータ20％に分割します。時系列データのためシャフルは行いません。

def split_data(data_array, datetime_array):

    m = len(data_array)

    train_batches = int(m * 0.8)
    # 80% training data(cv included), 20% test data

    m_train = train_batches
    time_train, time_test = datetime_array